Wonder Material, Part 3 – By Macron Beam to the Stars!

We’ve discussed the potential boost that quarter-wave sails made of Carbon Nano-Tubes (CNTs) might achieve from being pushed by the Sun. Dropping to 0.019 AU, the final velocity is 0.056c – dropping to 0.00465 AU (skimming the photosphere) would allow a speed of over 0.11c, but the material might not be up to the beating. Crewed vehicles would not endure the extreme acceleration – 84,000 gee at peak – so the speeds that might be achieved by solar-sailing star-travellers would be limited to 1,000 year flights to Alpha Centauri, with just 17 gee peak acceleration (as described in papers by Matloff).

Yet there is another option. Given a supply of small sails, carefully aimed or with some guidance, then why not use them as the momentum transfer system for a crewed starship? Greg Matloff explored the “macron beam” option in his discussion of non-nuclear starship propulsion in the early 1980s, but AFAIK didn’t suggest using mini-sails to accelerate larger starships. Jordin Kare proposed micro-sails pushed by laser to use as a momentum beam, but what I am suggesting is using very rugged solar-sails for boosting manned vehicles to higher speeds than their ‘natural’ acceleration limits would allow.

If CNT quarter-wave sails prove as agile as Christensen, Zubrin & Spieth have described, able to accelerate at 18 m/s² at Earth’s orbit, thus having a thrust/mass ratio of ~3,000, then they could form the basis of a naturally energised “Sail-Beam” or “Macron Beam”. The most energy efficient ratio of macron-particle to space-vehicle velocity is 2:1, which allows a macron beam total mass of 1/2 the space-vehicle to be used. If the peak speed is limited to 0.056 c, then the most efficient starship speed is 0.028 c. But we can go faster if we have plenty of sails, approaching the macron beam speed asymptotically. In theory a Macron Beam of mini-sails could push an Icarus Probe, with a payload of 150 tonnes, to the preferred mission speed of ~0.045 c.

I’ve derived a proof of the most efficient ratio, using an equation originally derived by Matloff – the proof is available here: Maximum Mass-Beam Efficiency

The basic equation is:

dV/V = 2.e.(M_p/M_s)/[1 + 2.e.(M_p/M_s)]

…where dV is the velocity change, V the macron beam speed, e the momentum transfer efficiency, M_p the total particle mass, and M_s the vehicle mass. If we rearrange it to find the ratio M_p/M_s, we get:

M_p/M_s = (dV/V)/[2.e.(1-dV/V)]

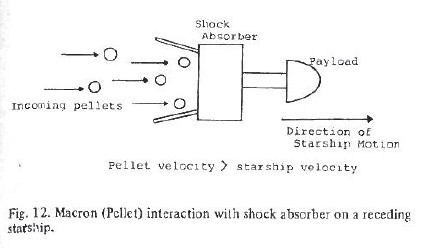
If we assume a perfect reflection (e = 1), then double the mass of the vehicle in Macron Beam mini-sails is needed to get to 0.045 c, with a Macron Beam speed of 0.056 c. As the mini-sail approaches the ship it’s zapped by a laser tuned to a frequency at which it absorbs strongly, quickly blasting it into plasma. Alternatively it is heated by smashing into the vehicle’s magnetic field at a high relative speed. Then the plasma is reflected from a magnetic mirror arrangement on the starship. Some will stream forward at the centre of the magnetic mirror, reducing the reflection efficiency slightly.

If the starship accelerates at 1 m/s² then it’ll need a final mass-flow of ~0.03 kg/s to push a 200 tonne starship. This doesn’t seem onerous. To reach 0.045 c will need 13,500,000 seconds – just over 156 days. The real trick is keeping the sails on course over ~600 AU when the acceleration finishes.