Power, Distance and Time are inextricably linked in rocketry. When leaving the Earth’s surface this is not so obvious, since all the sound and fury happens for a few minutes, and silence descends once the rocket enters orbit, free-falling indefinitely, at least until drag brings it back down. For slow journeys to the Moon, Near Earth Asteroids, Mars, Venus etc. the coasting Hohmann Transfer orbits and similar low-energy orbits, are all typically “sudden impulse” trajectories, where the engines fire for a few minutes to put a spacecraft on a months long trajectory.
For trips further afield – or faster journeys to the nearer planets – the acceleration time expands to a significant fraction of the total journey time. Ion-drives and solar-sails accelerate slowly for months on end, allowing missions like “Dawn” which has successfully orbited two Main Belt objects, Ceres and Vesta, all on one tank of propellant. Given more power an electrical propulsion system can propel vehicles to Mars in 2-3 months, Jupiter in a year and Saturn in under 2. Exactly how good the performance has to be is the subject of this post.
Firstly, an important concept is the Power-to-Mass ratio or specific power – units being kilowatts per kilogram (kW/kg). Any power source produces raw energy, which is then transformed into the work performed by the rocket jet. Between the two are several efficiency factors – the efficiency of converting raw heat into electricity, then electricity into jet-power, which includes the ionization efficiency, the nozzle efficiency, the magnetic field efficiency and so on. A solar array converts raw sunlight into electricity with an efficiency of between 20-25%, but advanced cells exist which might push this towards 40-50%.
Let’s assume a perfect power source and a perfect rocket engine. What’s the minimum performance required for a given mission? The basic minimum is:
Power/Mass is proportional to (S^2/T^3)
That is the Power-to-Mass ratio required is proportional to the displacement (distance) squared, and inversely proportional to the mission time cubed. For example, a 1 year mission to Jupiter requires 1,000 times the specific power of a 10 year mission.
The minimum acceleration case is when acceleration/deceleration is sustained over the whole mission time. When acceleration is constant, it means a maximum cruise speed (i.e. actual speed of vehicle) of 2 times the average speed (defined as total displacement divided by total mission time).
Another result, from a mathematical analysis I won’t go into here, is that the minimum specific power mission requires a cruise speed that is 1.5 times the average speed and an acceleration+deceleration time, t, that is 2/3 the total mission time T.
Remember that kinetic energy is 1/2.M.V^2, thus specific kinetic energy per unit mass is 1/2.V^2.
The power required – which is work done per unit time – is a trade off between acceleration time and mission time. Say the mission time is 10 years. If all the acceleration is done in 1 year, then the cruise speed required is 1/0.95 times the average speed, but power is proportional to the speed squared divided by the acceleration time: P = (1/2).V^2/t = (1/2).(1/0.95)^2/1 ~ 0.55, whereas in the case of constant acceleration, the average specific power is (1/2).(2)^2/10 = 0.2. For the case of minimum power it’s (1/2)*(3/2)^2/(2/3*10) = 0.16875 – just 84.375% the constant acceleration case and ~31% the 1 year thrust time.
So what does it take to get to Planet 9? If we use the distance of 700 AU to Planet 9, and a total trip time of 10 years, that means an average speed of 70 AU per year. To convert AU/yr to km/s, just multiply by 4.74 km/s, thus 331.8 km/s is needed. Cruise speed is then 497.7 km/s and the specific jet-power is 1.177 kW/kg, if we’re slowing down to go into orbit. Presently there are only conceptual designs for power sources that can achieve that sort of specific power. If we take 20 years to get there, the specific power is 0.147 kW/kg, which is a bit closer to possible.
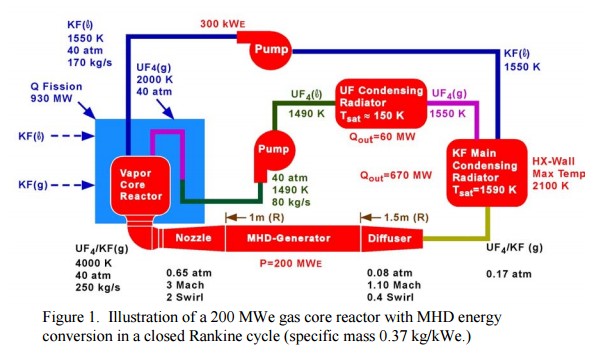
Space reactor designs typically boast a specific electrical power output of 50 W/kg to 100 W/kg. Gas-core nuclear reactors could go higher, putting out 2,000 – 500 W/kg, but our applied knowledge of gas-core reactors is limited. Designs exist, but no working prototypes have ever flown. In theory it would use uranium tetrafluoride (UF4) gas as the reacting core, which would run at ~4000 K or so and convert heat to electricity via a magnetohydrodynamic (MHD) generator. Huge radiators would be required and the overall efficiency of the power source would be ~22%. In fact there’s a theorem that any thermal power source in space has its highest specific power when the Carnot efficiency is just 25%, thanks to the need to minimise radiator area by maximising radiator temperature.
More exotic options would be the Fusion-Driven Rocket or a space-going stellarator or some such fusion reactor design with a high specific power. In that case it’d be operated more as a pure rocket than powering an electrical rocket. Of course there’s the old Orion option – the External Nuclear Pulse Rocket – but no one wants to put *potential* nuclear warheads into orbit, just yet.


Did you see this discussion?
http://forum.nasaspaceflight.com/index.php?topic=39382.0
I especially liked comment#6:
whitelancer64 on 01/20/2016 11:08 PM:
“Ad Astra did a study for a probe with a 2 to 8 megawatt nuclear reactor powered VASIMR engine that could get out to 1000 AU within 30 years.”
Something along those lines is probably the best bet.
Reply from a_langwich:
“While in theory it might get to 1000 AU within 30 years, in practice it won’t launch within the next 100 years.”
I share the opinion that an earlier launch date using solar thermal and the Oberth effect could get there sooner than longer to develop, later to launch, and no doubt more expensive nuclear propulsion concepts, though a later orbital mission – as opposed to a simple flyby mission – would need more advanced propulsion.
I like the E-Sail concept, though a solar-sail might do it too. The real impediment is the slow plodding by the bureaucracies.