Black Holes are fundamentally simple objects. Their size is the Schwarzschild Radius, calculated as:
$$Rs\ = \frac{2\mu}{c^2}$$
where \(mu\) is the mass times the Newtonian Constant G, and c the speed of light. Substituting into the Newtonian equation for surface gravity gives the following:
$$g_s\ = \frac{c^4}{4\mu}$$
From a distance much greater than the radius of the Black Hole, the acceleration appears infinite. Only locally is it finite. For a 1 solar mass star the acceleration is over 6.2 trillion gees. The time an infalling observer experiences before colliding with the singularity is:
$$t\ = \frac{\pi\mu}{c^3}$$
For a 1 solar mass hole it’s just a few millionths of a second. But a billion solar mass hole, it’s hours. Space-time infalls towards the singularity at faster than light, which is why nothing escapes. At the singularity the space-time is hard to see for binocular vision equipped beings like humans. A trinocular being would see clearly – perhaps the Third Eye has a space-time meaning?

Acceleration however is not the appropriate value to define what happens to an infalling observer. Tidal forces are what are felt – the force per metre exerted by the changing acceleration. The acceleration of the acceleration, so to speak. For lateral tidal force the value is computed by:
$$g’ = \frac{c^6}{4\mu^2}$$
which has the value of 10^10 m/s2/m at the Event Horizon of a Solar Mass black hole. A billion Solar Mass black hole has tidal forces of just 10-8 m/s2/m at the Event Horizon – basically negligible. For reference, 1 gee per metre is the equivalent of holding your arms out and spinning once every two seconds – i.e. 30 rpm. Spinning 10 times quicker, at 300 rpm, you’ll experience 100 gee per metre along your arms, which you’d experience crossing the Event Horizon of a 10,000 Solar mass black hole.
Professor Andrew Hamilton covers the experience of falling into various types of Black Hole at his web-site here:
Journey into a Schwarzschild Black Hole
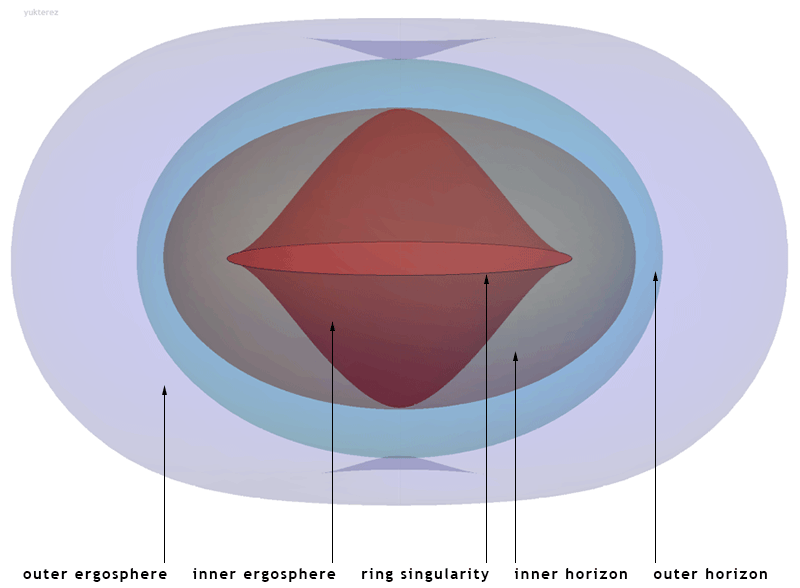
Rotating Black Holes feature a ring of ultra-compressed matter – the remains of the collapsed star. More likely the collapse process produces the object at the centre of the above diagram, with the “ring” being the edge of the whole object. Super-compressed matter wraps itself in tortured space-time which would be lethally full of energy.
Inside the black hole – but outside the collapsing mass – orbits are possible and planets might exist there…
Orbits Within Black Holes